There are six trigonometric functions: sin (sine), cos (cosine), tan (tangent), csc (cosecant), sec (secant), and cot (cotangent).
These functions represent the relationship between the initial side of the angle and the terminal side.
In standard position, the initial side lies along the positive x-axis and the terminal side lies anywhere and is what defines the angle.
Let θ be an angle in standard position formed by the initial side (x) and the terminal side formed by the point (x,y) when r = √(x²+y²) ≠ 0
sin θ = y/r
cos θ = x/r
tan θ = y/x, x≠0
csc θ = r/y, y≠0
sec θ = r/x, x≠0
cot θ = x/y, y≠0
As you can see from these relationships, each of the trigonometric functions has their respective reciprocals. The reciprocal pairings are sin θ and csc θ, cos θ and sec θ, and tan θ and cot θ.
e.g 1/sin θ = csc θ and 1/csc θ = sin θ
As you can see from these relationships, each of the trigonometric functions has their respective reciprocals. The reciprocal pairings are sin θ and csc θ, cos θ and sec θ, and tan θ and cot θ.
e.g 1/sin θ = csc θ and 1/csc θ = sin θ
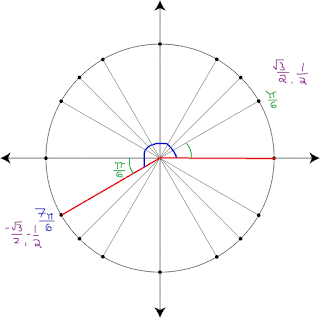
For each terminal side of an angle, there is a corresponding angle that is called the reference angle. The reference angle is the angle formed by the terminal side of the angle and the x-axis.
(http://calculator.tutorvista.com/reference-angle-calculator.html)
*For angles in the 1st quadrant, the angle is its own reference angle.
The reason that reference angles are used in trigonometry is that an angle and it's reference angle have equal trigonometric function values, although the sign value of the value can vary. This is useful when evaluating trigonometric functions because you can simplify your value and use the quadrant location to determine the corresponding functions.
EXAMPLE:
The cosine of 7π/6 is ⁻√3/2 and it's reference angle, π/6 has a cosine of √3/2. Since, 7π/6 lies in the 3rd quadrant, we can determine that it's x value (cosine value) is negative.


No comments:
Post a Comment