Chapter 4 Review

 Chapter 4

Chapter 4 focuses on trigonometric functions.

4.1 - Radian and Degree Measure

Angle: two rays with a common endpoint

Angles are measured in degrees or radians.

• To convert to degrees, multiply radians by    

• To convert to radians, multiply degrees by     

To obtain the length of an arc length, you can use the equation  , where s = arc length, r = radians, and  = the angle measure in radians.

• When two angles are supplementary, their measures add up to 180 degrees
• When two angles are complementary, their measures add up to 90 degrees
• When angles are congruent, they have the same measure
• When angles are coterminal, they have the same initial and ending sides.

4.2 - The Unit Circle

The unit circle has a radius of one, and can be used to solve trigonometric functions of angles.

The sin value corresponds to the y-coordinate on the unit circle, and the cos value corresponds to the x-coordinate.

For example, the angle  has a sin value of  , and a cos value of 

Cosine and secant functions are even, which means that

 

4.3 - Right Triangle Trigonometry

Using the various trigonometric functions and the rules of SOHCAHTOA, it's possible to find side lengths or angles of right triangles.

• When you are looking for a trigonometric function that is different from the ones you have, the trigonometric identities that relate them can be used.

• Using these identities, you can transform one side of an equation to the other by only manipulating one side.

   

1 = 1

4.4 - Trigonometric Functions of Any Angle

Any angle  on the unit circle has x and y values for each trigonometric function

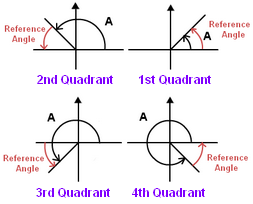
On the unit circle, reference angles can be found by evaluating the angle between the x - axis and the terminal side of an angle. They're always acute, and differ for each quadrant

For example, for an angle  in Quadrant II, you would find the reference angle with 

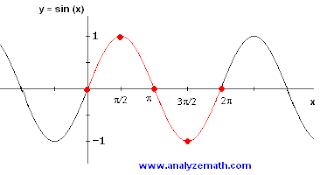
4.5 - Graphs of Sine and Cosine Functions

When the graph makes one full cycle, it is called the period.

The equations for the sin and cos graphs are

y = a sin (bx - c) + d

y = a cos (bx - c) + d

________________________________________________________________

a = the amplitude of the function (vertical stretching). It basically tells you how high and low the graph should reach

b = the value that helps to find the period. For sin and cos, the period is 

c = phase shift (horizontal shifting). When subtracting c, the graphs shifts right. When adding it, it shifts left.

d = vertical shift

_______________________________________________________________________________

4.6 - Graphs of Other Trigonometric Functions

The graphs of tan, cot, sec, and csc share the same equation as the sin and cos graphs

* In the tan and cot graphs, the period is determined by   

  

  The csc and sec graphs run tangent to the sin and cos graphs, so it may be useful to graph those functions as well.

4.7 - Inverse Trigonometric Functions

When we restrict the domain of  y = sin x to      , we can use the inverse sin function, denoted by 

This can be done with all six functions

THE OUTPUT OF AN INVERSE TRIG FUNCTION SHOULD ALWAYS BE AN ANGLE MEASURE

Inverse functions may also be denoted with y = arcsin x,  y = arccos x, etc.

In a triangle such as this, we can use inverse functions to find 

4.8 - Applications and Models

There are many pointless ways to apply trigonometric functions in real life.

Bearings:

Since bearings are usually given in degrees, it's a natural fit for trigonometry.

Bearings are typically written like this:  N  43° E  

This means 43° north of east

Angles of Elevation/depression:

Many story problems call for an angle to something higher or lower than another object

Using this angle is typically required for such problems, as it can be used to find other values.

For example, the angle of elevation (48°), can be used along with the tangent function to find x.

x = 20 ft.