Section 2.1: Quadratic Functions
Polynomial functions:
Definition:
is a polynomial function of x with degree n
Polynomial functions are classified by degree:
The function
Degree Name
0 Constant
1 Linear
2 Quadratic
3 Cubic
4 Quartic
5 5th degree
Quadratic Functions:
Let a, b, and c be real numbers, where a can't be zero
is called a quadratic function
is the vertex form, where the vertex is represented as (h,k).
If a > 0, the parabola opens upward
If a < 0, the parabola opens downward
Completing the square can be used to solve quadratic equations:
1. Write original function, in standard form.
2. Divide all terms by the leading coefficient of the first term.
3. Divide the value of b by 2, then square it.
4. Move the value c to the very right of the equation.
5. Add/subtract the value from step 3 to the first two terms, the do the opposite to the value of c, all the way on the right.
6. Factor the perfect square and regroup terms.
Section 2.2: Polynomial Functions of Higher Degrees
Leading Coefficient Test:
As x moves without bound to the left or right, the graph of a polynomial function with degree n rises or falls in the following manner:
When n is odd:
f(x) approaches infinity as x approaches infinity
If the leading coefficient is positive, the graph falls to the left and rises to the right
If it's negative, the opposite is true
When n is even:
f(x) approaches negative infinity as x approaches infinity, and vice versa
If the leading coefficient is positive, the graph rises to the left and right
If the leading coefficient is negative, the graph falls to the left and right
Zeroes of polynomial functions:
For the polynomial function f of degree n, the following is true:
1. The graph of f has, at most, n real zeroes
2. The function f has at most n-1 relative extrema (relative minimums or maximums)
Real Zeroes:
If f is a polynomial function and a is a real number, the following statements are true:
1. x=a is a zero of the function f
2. x=a is a solution of the polynomial function f(x)=0
3. (x-a) is a factor of the polynomial f(x)
4. (a,0) is an x-interecept of the graph f
Section 2.3: Real zeroes of polynomial functions
The division algorithm:
If f(x) and d(x) are polynomials such that d(x) doesn't equal zero< and the degree of d(x) is less than or equal to the degree of f(x), there exist unique polynomials q(x) and r(x) such that
f(x) = d(x)q(x) + r(x)
Where f(x) is the dividend
d(x) is the divisor
q(x) is the quotient
and r(x) is the remainder
Rational Zero Test:
If the polynomial f(x) has integer coefficients, every rational zero of f has the form
Rational Zero = p/q
Where p and q have no common factors other than 1, p is a factor of the last term, and q is a factor of the leading coefficient
Upper and Lower Bound Rule:
Let f(x) be a polynomial with real coefficients and a positive leading coefficient. Suppose f(x) is divided by x - c using long division.
1. If c > 0 and each number in the last row is either positive or zero, c is an upper bound for the real zeroes of f
2. If c < 0 and the numbers in the last row are alternately positive and negative, c is a lower bound for the real zeroes of f
1. Long Division
The process is similar to long dividing integers.Example:
Set up the equation as you would in a regular long division problem
Divide the leading term of the dividend by the leading term of the divisor
Multiply the x by both terms in the divisor and place the product directly underneath the terms with the corresponding power
Just like regular long division, subtract the product from the terms above, leaving you with a single term
Bring down the next term, 10, and repeat the process of dividing the leading term by x, giving you -10
Multiply x and 1 by to give you the remaining product
Once again, subtract the product from above to finish the equation. Above the long division sign if your quotient, x-10.
If the last step of subtraction does not equal zero, the equation has a remainder.
In this case, you take the number left over and put it over the divisor of the equation, giving you the remainder.
Example:
with a remainder of -7
So the final answer is
2. Synthetic Division
Example:
Put the coefficients at the top of a flipped division sign
Put 1, the known zero of the function, outside the box
Bring down the leading coefficient. Multiply the number by the zero and put the product below the next coefficient
Add the numbers in the column and multiply the sum by the zero. Place that product under the next coefficient
Again, add the numbers in the new column. If the last column equals 0, the solution has no remainder. In this case, there is a remainder of 12
Final Answer:
Section 2.4: Complex Numbers
Certain quadratic equations have no real solutions. This is why they created the imaginary unit i which is defined as 
where 
. A set of complex numbers is created by adding real numbers to real multiples of the imaginary unit. When a complex number is written 
it is in standard form.
Definition of a complex number:
where . A set of complex numbers is created by adding real numbers to real multiples of the imaginary unit. When a complex number is written it is in standard form. Definition of a complex number:
If a and b are real numbers, the number a + bi is a complex number, and it is said to be written in standard form. If b = 0, the number a + bi = 0 is a real number. If b does not equal zero, the number a + bi is called an imaginary number. A number of the form bi, where b does not equal zero, is called a pure imaginary number.
Addition and Subtraction of Complex Numbers:
If and 
are two complex numbers in standard form then the definition of addition and subtraction is:
Sum:
Example:
Addition and Subtraction of Complex Numbers:
If
and are two complex numbers in standard form then the definition of addition and subtraction is:Sum:
Example:
Difference: 
Example:
Multiplying and Dividing Complex Numbers:
In order to multiply complex numbers in standard form, it is important to use the distributive property or also known as the FOIL method.
Multiplication:
Example:
Example:
Multiplying and Dividing Complex Numbers:
In order to multiply complex numbers in standard form, it is important to use the distributive property or also known as the FOIL method.
Multiplication:
Example:
The equation below is not in standard form:
Because we can use that to change the equation to standard form
we can use that to change the equation to standard form
Final answer in standard form:
In division, in order to not have i in the denominator of the equation we use the complex conjugate (conjugate of the denominator) to solve the equation by multiplying it to the numerator and denominator of the original equation.
Division:
Example:
Multiplying by the complex conjugate:
Answer not in standard form yet
Final answer in standard form:
Imaginary Number Helpful Facts:
The answers of the equations come in full circle after four. This helps if you need to solve a problem like:
Because the answers rotate every four, divide the number by 4
The remainder will tell you the answer of the question.
Because and the remainder of the equation is 3:
and the remainder of the equation is 3:
Section 2.5: The Fundamental Theorem of Algebra
In the complex number system, every nth-degree polynomial function has exactly n zeros. This is derived from the Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra - If f(x) is a polynomial of degree n, where n > 0, f has at least one zero in the complex number system.
The fundamental theorem of algebra also gives you the linear factorization theorem.
Linear Factorization Theorem - If f(x) is a polynomial of degree n where n > 0, f has precisely n linear factors
Where c1, c2, . . . , cn are complex numbers
Real and Complex Zeros of Polynomial Functions
Example:
This polynomial can be factored into:
This shows that the zeros are
(x-2) with a multiplicity of two, (x-2i) and (x+2i)
Notice that (x-2) is listed twice and (x-2i) and (x+2i) are both complex zeros.
Remember:
***The n zeros of a polynomial function can be real or complex and they may be repeated***
***Imaginary roots always come in conjugate pairs***
Finding the Zeros of a Polynomial Function
Example:
The possible rational zeros of this polynomial function are ±1, ±2, ±4, and ±8
(Find these by taking factors of the constant divided by the factors of the leading coefficient. The leading coefficient is 1 so we only need the factors of the constant)
By graphing this function, you can see that -2 and 1 are both real zeros.
***Only the real zeros are shown on the graph as x-intercepts***
After finding the real zeros, you can find the imaginary zeros by using synthetic division.
Using -2 and 1 twice you are left with:
To find the zeros we need to factor this
This gives us the remaining non-real zeros. All five zeros of this polynomial are:
1, 1, -2, 2i, and -2i
Conjugate Pairs:
In the last example two of the zeros were -2i and 2i. This is because all imaginary roots must come in conjugate pairs, in the form a + bi and a - bi
In a polynomial function with real coefficients if a + bi is a zero of the function and b is not 0 then the conjugate a - bi must also be a zero of the function.
Finding a Polynomial with Given Zeros:
Given the degree of a polynomial function with real coefficients and its zeros we can easily determine the polynomial.
Example:
The Fundamental Theorem of Algebra - If f(x) is a polynomial of degree n, where n > 0, f has at least one zero in the complex number system.
The fundamental theorem of algebra also gives you the linear factorization theorem.
Linear Factorization Theorem - If f(x) is a polynomial of degree n where n > 0, f has precisely n linear factors
Where c1, c2, . . . , cn are complex numbers
Real and Complex Zeros of Polynomial Functions
Example:
This polynomial can be factored into:
This shows that the zeros are
(x-2) with a multiplicity of two, (x-2i) and (x+2i)
Notice that (x-2) is listed twice and (x-2i) and (x+2i) are both complex zeros.
Remember:
***The n zeros of a polynomial function can be real or complex and they may be repeated***
***Imaginary roots always come in conjugate pairs***
Finding the Zeros of a Polynomial Function
Example:
The possible rational zeros of this polynomial function are ±1, ±2, ±4, and ±8
(Find these by taking factors of the constant divided by the factors of the leading coefficient. The leading coefficient is 1 so we only need the factors of the constant)
By graphing this function, you can see that -2 and 1 are both real zeros.
***Only the real zeros are shown on the graph as x-intercepts***
After finding the real zeros, you can find the imaginary zeros by using synthetic division.
Using -2 and 1 twice you are left with:
To find the zeros we need to factor this
This gives us the remaining non-real zeros. All five zeros of this polynomial are:
1, 1, -2, 2i, and -2i
Conjugate Pairs:
In the last example two of the zeros were -2i and 2i. This is because all imaginary roots must come in conjugate pairs, in the form a + bi and a - bi
In a polynomial function with real coefficients if a + bi is a zero of the function and b is not 0 then the conjugate a - bi must also be a zero of the function.
Finding a Polynomial with Given Zeros:
Given the degree of a polynomial function with real coefficients and its zeros we can easily determine the polynomial.
Example:
A third degree polynomial function with real coefficients has 2 and 4i as zeros. Given 4i as a zero we know that -4i must also be a zero. Because the polynomial function is a third degree function we now have all the zeros: 2, 4i, and -4i.
We can write these out as:
To get the original polynomial we can multiply these factors.
This results in:
Factoring A Polynomial
Factors of a Polynomial - Every Polynomial of degree n > 0 with real coefficients can be written as the product of linear and quadratic factors with real coefficients, where the quadratic factors have no real zeros.
Example:
This can be factored into two quadratic polynomials
This can be further factored to include imaginary numbers
Zeros of a Polynomial Function
Given one complex zero of a polynomial function we can find the remaining zeros.
Example:
5i is a zero of
Because 5i is a complex number, we know that -5i must also be a zero of this polynomial because all complex zeros come in conjugate pairs.
We can multiply these together to get part of the polynomial:
We can now use long division using this to find the remaining zero.
/
This gives us
The zeros of this polynomial are:
Section 2.6: Rational Functions and Asymptotes
A rational number is a number that can be written in a ratio.
A rational function is a function that can be written as:
In this, N and D are both polynomials.
The domain of f is all numbers that do not make the denominator equal to 0.
Example 1.
Find the domain of
Solution: Factor the denominator. (x+3)(x-3)
Solve to find values of x that make the denominator = 0, x=3,-3
Domain: all real numbers except -3 and 3,
Horizontal and Vertical Asymptotes
Definitions of Asymptotes
1. A graph has a vertical asymptote if D(x)=0. This means that all values that are not in the domain are vertical asymptotes.
2. A horizontal line is a horizontal asymptote of the graph if the graph approaches the line as x approaches positive or negative infinity.
The graph will never cross a vertical asymptote, but it may cross a horizontal asymptote
Rules for Asymptotes of Rational Functions
Let f be a rational function:
1. The graph of f has a vertical asymptote at x = a if D(a) = 0. A vertical asymptote occurs at the value(s) of x that make the denominator equal to 0, which makes the function undefined.
2. The graph of f has one horizontal asymptote or no horizontal asymptote, depending on the degree of N and D.
a. If the degree of the numerator (n) is less than the degree of the denominator(m), then the horizontal asymptote is y=0.
b. If the degree of the numerator (n) is equal to the degree of the denominator(m), then the horizontal asymptote is quotient of the leading coefficients.
c. If the degree of the numerator (n) is greater than the degree of the denominator (m), then there is no horizontal asymptote.
3. The graph of f has a slant asymptote if the degree of the numerator (n) is 1 greater the degree of the denominator (m).
Example 2.
Find any horizontal and vertical asymptotes of the following.
Solution: The degree of the numerator is 1 and the degree of the denominator is 1. Since the degree of the numerator is equal to than the degree of the denominator, the horizontal asymptote is the quotient of the leading coefficient of the numerator and the denominator, so it is:
Set the denominator equal to zero and solve for x.
4x-6=0, so the vertical asymptote is:
Set the denominator equal to zero and solve for x.
X2-1=0
X=1,-1, so the vertical asymptotes are x=1 and x=-1
Section 2.7: Graphs of Rational Functions
How to graph a rational function:
1. Find and plot the y-intercept by evaluating f(0).
2. Set the numerator equal to zero and solve to find the x-intercepts.
3. Set the denominator equal to zero to find the vertical asymptotes.
4. Find and sketch the horizontal asymptote if there is one.
5. Use curves to complete the graph between and after the vertical asymptotes.
Example:
1. Find and plot the y-intercept by evaluating f(0).
2. Set the numerator equal to zero and solve to find the x-intercepts.
3. Set the denominator equal to zero to find the vertical asymptotes.
4. Find and sketch the horizontal asymptote if there is one.
5. Use curves to complete the graph between and after the vertical asymptotes.
Example:
Find the y-intercept by plugging in 0 for x. You then find f(0)=5, therefore making the y-intercept (0,5).
Now to find the x-intercepts set the numerator equal to 0.
0=5+2x
x= -5/2
This tells you that the x-intercept in (-5/2,0)
To then find the vertical asymptote you must set the denominator equal to 0. From here we can see that the vertical asymptote is line x= -1.
From the information above we can also see that the horizontal asymptote is line y=2
Most of the time with vertical asymptotes, the two parts are on different ends of the asymptote, for example the graph above. Although when you have a vertical asymptote with a multiplicity of two, they are on the same end.
Example:
This has a multiplicity of 2 at the asymptote x=1.
Some graphs can also have holes. When there are the same factors located in the numerator and the denominator of the function it cause a hole at that x value in the graph.
Example:
With this on the graph we should see a hole when x=1 due to the same factor in the numerator and denominator.
Slant Asymptotes:
If the degree of the numerator is one more than the degree of the denominator then the function has a slant asymptote. To find the line of the asymptote you must use long division and divide the numerator by the denominator.
Example:
This divides out to x-2 with a remainder of 2. The slant asymptote is the line f(x)=x-2.
0=5+2x
x= -5/2
This tells you that the x-intercept in (-5/2,0)
To then find the vertical asymptote you must set the denominator equal to 0. From here we can see that the vertical asymptote is line x= -1.
From the information above we can also see that the horizontal asymptote is line y=2
Example:
This has a multiplicity of 2 at the asymptote x=1.
Example:
With this on the graph we should see a hole when x=1 due to the same factor in the numerator and denominator.
Slant Asymptotes:
If the degree of the numerator is one more than the degree of the denominator then the function has a slant asymptote. To find the line of the asymptote you must use long division and divide the numerator by the denominator.
Example:
This divides out to x-2 with a remainder of 2. The slant asymptote is the line f(x)=x-2.
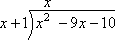
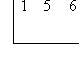
No comments:
Post a Comment