In section 1.1 we covered Functions.
Definition of a Function: A function f from set A to set B is a relation that assigns to each element x in the set A exactly one element y in the set B. Set A is the domain (or set of inputs) of the function f, and the set B contains the range (or set of outputs).
For every input, there can be one or more outputs. But one output cannot have multiple inputs, or else it is not a function.
Testing for Functions Algebraically
Solving for functions algebraically is making sure that y is a function of x. This is done by solving for y in terms of x. For example:
This function can be Since there are two possible values of y, this
algebraically solved to show is not a function
that for every x value there is
one y value, making it a function
Piecewise Functions:
When x is less than zero we use the equation
When x is greater than or equal to zero we use the equation
When x is greater than or equal to zero we use the equation
Determining the Domain of a Function:
The domain of a function is the set of all values of the independent variable for which a function is defined. Any x value that is not in the domain of f is considered undefined. The implied domain is the set of all real numbers for which the expression is defined.
The Difference Quotient:
The Difference Quotient is the equation
which is a fundamental calculus definition.This is the definition simplified, an example is below
After simplifying this definition down, the final answer would be 2x+h+2
In section 1.2 we covered Graphs of Functions:
The Graph of a Function f is a collection of ordered pairs (x, f(x)) such that x is the domain of f. Remember that x= the directed distance from the y-axis, and f(x)= the directed distance from the x-axisThe domain and range of a function can be determined algebraically or graphically.
For example:
Algebraically, the function
has a domain that is greater than or equal to zero because x is under a radical. Then by solving for 
, you determine that x has to be greater than or equal to 16. This means that the domain of the function is 
. The range of the function is all real numbers greater than zero because the radical prevents any negative range value.Graphically, it is best to plug the function into the calculators Y= button and determine the domain and range of the function.
Vertical Line Test:
When you make a graph of a collection of ordered pairs, the easiest way to determine if the ordered pairs is a function is using the Vertical Line Test.
The Vertical Line Test definition is as follows: A set of points in a coordinate plane is the graph of y as a function of x if and only if no vertical line intersects the graph at more than one point.
A visual representation of this is
Next in 1.2 are the definitions of increasing, decreasing, and constant functions.
Following the definitions of the different kind of functions, there were the definitions of relative minimum and maximum values.
A function value f(a) is called a relative minimum of f if there exists an interval 
that contains a such that
implies 
that contains a such that implies
A function value f(a) is called a relative maximum of f if there exist an interval 
that contains a such that implies 
that contains a such that implies
Lastly in 1.2, we discovered how to determine if a function is Even or Odd.
How to test for an Even or Odd function:
A function f is Even if, for each x in the domain of f, f(-x)=f(x)
A function f is Odd if, for each x in the domain of f, f(-x)=-f(x)
To determine if a function is Even or Odd graphically, just look at the function's graph. If its graph is symmetrical with respect to the origin, it is Odd. If its graph is symmetrical with respect to the y-axis, it is Even.
To determine if a function is Even or Odd algebraically, you have to substitute in values for f(x). If you substitute in -x for x in f(x) and get f(x)=f(-x) then the function is Even. If you substitute in -x for x in f(x) and get f(-x)=-f(x) then the function is Odd.
In section 1.3 we covered Shifting, Reflecting, and Stretching Graphs
The basic function that is used for all transformations on a graph is
In this function,
a=vertical stretch/compress
b=horizontal stretch/compress
c=horizontal translation
d=vertical translation
Keep in mind that b is a stretch if it is less than 1, and a compress if greater than 1. Also, a is a stretch if it greater than 1, and a compress if less than 1.
Consider the parent function
Its graph looks like this
All of the translations from the function are represented on this graph
are represented on this graph
The parent function is represented by the black in the middle.
is represented by the black in the middle.
The vertical shift of d is represented in red on the graph and is shifted down by -2.
The horizontal shift of c is represented in brown on the graph and is shifted right by 2.
The horizontal stretch of b is represented in blue on the graph by a factor of 1/2.
The vertical stretch of a is represented in green on the graph by a factor of 2.
Other than these transformations, graphs of functions can be reflected by being multiplied by a negative number. For example the graph of 
in green looks like this compared to the parent function.
in green looks like this compared to the parent function.
In section 1.4 we covered Combinations of Functions
There are four main combinations of functions. These are the sum, difference, product, and quotient of functions.
Examples: 
and 
and
Sum: 
Difference: 
Product:
Quotient:
= 5 remainder -8
These are the four basic combinations of functions. Here are their definitions.
Another combination of functions is the composition of a function.
Definition:
The composition of the function f with g is 
=
, the domain of f of g is the set of all the x in the domain of g such that g(x) is in the domain of f.
=, the domain of f of g is the set of all the x in the domain of g such that g(x) is in the domain of f.
Example
=
In section 1.5 we covered Inverse Functions
Inverse Functions:
There are two ways to verify inverse functions. Algebraically and Graphically. Graphically in order to verify an inverse function you need to graph the original function and the inverse function. If their graphs are symmetrical among the line y=x then they are inverses of each other. If they are not then the functions are not inverses of each other. Algebraically involves creating a composition of the two functions that are in question. If they both equal x then they are inverses of each other. If it equals something else, then they are not inverses of each other.
Here is an example the book provides
Other than inverse functions in section 1.5, one-to-one functions are noted.
Definition of one-to-one:
A function f is one-to-one if, for a and b in its domain, 
implies a=b
implies a=b
Also, a function only has an inverse if it is one-to-one.
If you substitute in a and b for x in a function and they end up equaling each other, then it is one-to-one.
To verify this graphically, use the horizontal line test. This is similar to the vertical line test, except the line is horizontal. If it intersects more than one point then the function is not one-to-one.
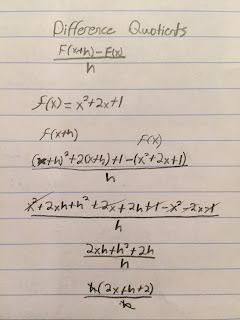
No comments:
Post a Comment