Chapter 5.4 - The Sum and Difference Formulas

Today in class we discussed and derived the sum and difference formulas for the three main trigonometric functions (sine, cosine, and tangent).

Before we jump right into the actual deriving of the formulas, let's review what the formulas actually are.

Sine:

Cosine:

Note: While the addition/subtraction signs correspond in the sine functions, they aren't the same for cosine.

Tangent: 

Now we will derive the above formulas (not all of them) so we can see where they come from and why they are the way that they are. 

Deriving the Sine Formula

First, draw the following picture.

(Angle DFC is a right angle but it is missing the little box indicating a right angle)

What we are trying to do is create a formula that allows us to easily find the sine the angle at point A, which is x + y. 

Now, think about the first step that we would take to find the sine of (x + y). 

Sine is opposite over hypotenuse. The opposite side is leg DE and the hypotenuse is AD. 

Therefore,

Based on the length adding postulate, DE can become DF + FE. FE is the same as CB, so we can substitute that which gets you:

Now, it gets tricky. DF and CB mean absolutely nothing to us if we're thinking in trig form, so now we have to switch our brains to see these side lengths as trigonometric functions.  

Refer back to the initial triangle: 

(Angle DFC is a right angle but it is missing the little box indicating a right angle)

According to ∆CDF : the cosx = (DF / DC) 

Multiply each side by DC and you have DCcosx = DF which is part of the equation we're looking to replace. 

The same goes for ∆ABC : sinx = (CB / AC) which simplifies to ACsinx = CB

Now, the equation is starting to look a little bit more familiar:

We do the exact same steps to get rid of the DC and the AC in the numerator now. 

∆ACD : siny =  (DC / AD) so ADsiny = DC

and

∆ACD : cosy = (AC / AD) so ADsiny = AC

Substitute those in:

Divide out the 'AD's:

And there you go, one of the two sine sum and difference formulas. 

Following the same path, we can deduce that:

Deriving the Tangent Formula:

Don't worry, no more triangles for now. 

We know based on previous knowledge that tangent of any angle is the same as the sine of that angle divided by its cosine. 

There fore, we can conclude that:

Now, it's down to some basic algebraic principles of substitution and simplifying to find the easy tangent formula. 

By substituting into the addition formula we get:

To simplify this into all tangents, rather than a jumble of sines and cosines, we will multiply each side by one over cosxcosy as so:

Now, we have all sines and cosines without a jumble of different angles multiplied by each other. All we do is simplify into tangents and we have the completed formula:

Following the same path we can conclude that:

How to use the formulas:

These formulas can be used to find a trigonometric function that is not labelled on the unit circle.
Take π/12 for example, it's not a point on the unit circle, but we want to find out the sine value. In order to do this, one must find two values that add up or have a difference of π/12. 

Follow these steps:

Note: The answer to the last example should have a denominator of 4, not 2. (Sorry for the mistake).

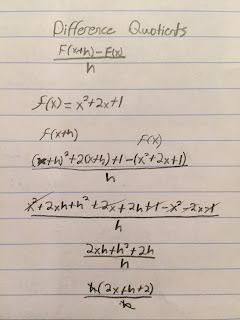
Capter 3 Review

Chapter 3 Review
Chapter 3 is about Logarithmic and Exponential Functions

3.1-Exponential Functions and Their Graphs

A basic Exponential Function is written as  
Where a>0  and a doesn't equal 1.
It's graph is as shown. It is an infinite domain, but a range of only 0 to infinity.

The graph of  can be transformed in 4 different ways. To illustrate this can be used.
Where a = vertical stretch of the function
           b = a sharper turn for higher b and a shallower turn for lower b
           c = horizontal shift of the function in the inverse direction of b's sign
           d = vertical shift of the function

3.2-Logarithmic Functions and Their Graphs

A basic Logarithmic Function is written as
Where a>0, x>0 and a doesn't equal 1.
Also, if and only if  does .
It is the inverse function of the basic exponential function and looks like this. Its range is negative infinity to 1 and its domain is 0 to infinity.


Common Log:
Natural Log:

The graph of can be transformed in 4 different ways. To illustrate thiscan be used.
Where a = vertical stretch of the function
           b = a sharper turn for higher b and a shallower turn for lower b
           c = horizontal shift of the function in the inverse direction of b's sign
           d = vertical shift of the function

 

3.3-Properties of Logarithms

Change of Base Formula:

If a, b, and x are positive real numbers and a and b don't equal 1. Then

This works for any base that is convenient as long as the bottom of the fraction is taking some sort of log of the initial base.

Properties of Logarithms:

Let a be a positive real number that doesn't equal 1, and let n be a real number as well. If u and v are positive real numbers, the following properties are true.

3.4-Solving Exponential and Logarithmic Equations

There are two basic strategies to solving exponential and logarithmic equations, the one-to-one property and the inverse properties.

One-to-One Properties:
 if and only if x=y.
if and only if x=y.
This property states that there is only one x value for every y value and therefore the log of a number or something taken to a number's power must equal other logs with the same base and other exponents with the same base.

Inverse  Properties:

This property states that a log taken of the base number is equal to the base number's power. This works along the same lines of 2/(2*4) because logs are the inverse operation of exponents just like division is the inverse operation of multiplication.


To solve a Logarithmic Equation in the easiest way, first write it in exponential form. Then use one-to-one or inverse properties as necessary to simplify the equation.

3.5-Exponential and Logarithmic Models
Mathematical models are equations and applications of math that are used to figure out parts of the real world. There are five common types involving exponential and logarithmic functions.

1. Exponential Growth:


2. Exponential Decay:

3. Gaussian Model:


4. Logistic Growth:


5. Logarithmic:

Chapter 1: Functions and Their Graphs

In section 1.1 we covered Functions.

Definition of a Function:  A function f from set A to set B is a relation that assigns to each element x in the set A exactly one element y in the set B.  Set A is the domain (or set of inputs) of the function f, and the set B contains the range (or set of outputs).

For every input, there can be one or more outputs.  But one output cannot have multiple inputs, or else it is not a function.

Testing for Functions Algebraically

Solving for functions algebraically is making sure that y is a function of x.  This is done by solving for y in terms of x.  For example:

1)                              2)

 

                                  

 This function can be                               Since there are two possible values of y, this
algebraically solved to show                   is not a function
that for every x value there is
one y value, making it a function      

Piecewise Functions:

Solve the function for x= -3, 0, 2

When x is less than zero we use the equation

When x is greater than or equal to zero we use the equation     

When x is greater than or equal to zero we use the equation

Determining the Domain of a Function:
The domain of a function is the set of all values of the independent variable for which a function is defined.  Any x value that is not in the domain of f  is considered undefined.  The implied domain is the set of all real numbers for which the expression is defined. 

The Difference Quotient:
The Difference Quotient is the equation  which is a fundamental calculus definition.

This is the definition simplified, an example is below

 

After simplifying this definition down, the final answer would be 2x+h+2

 

In section 1.2 we covered Graphs of Functions:

The Graph of a Function f  is a collection of ordered pairs (x, f(x)) such that x is the domain of f.  Remember that x= the directed distance from the y-axis, and f(x)= the directed distance from the x-axis

The domain and range of a function can be determined algebraically or graphically.
For example:
Algebraically, the function  has a domain that is greater than or equal to zero because x is under a radical.  Then by solving for , you determine that x has to be greater than or equal to 16.  This means that the domain of the function is .  The range of the function is all real numbers greater than zero because the radical prevents any negative range value.
Graphically, it is best to plug the function into the calculators Y= button and determine the domain and range of the function.

Vertical Line Test:
When you make a graph of a collection of ordered pairs, the easiest way to determine if the ordered pairs is a function is using the Vertical Line Test.

The Vertical Line Test definition is as follows: A set of points in a coordinate plane is the graph of y as a function of x if and only if no vertical line intersects the graph at more than one point.

A visual representation of this is

 

Next in 1.2 are the definitions of increasing, decreasing, and constant functions.



 Following the definitions of the different kind of functions, there were the definitions of relative minimum and maximum values.

 

A function value f(a) is called a relative minimum of f if there exists an interval  that contains a such that implies

 

A function value f(a) is called a relative maximum of f if there exist an interval  that contains a such that  implies

 

Lastly in 1.2, we discovered how to determine if a function is Even or Odd.

 

How to test for an Even or Odd function: 

A function f is Even if, for each x in the domain of f, f(-x)=f(x)

A function f is Odd if, for each x in the domain of f, f(-x)=-f(x)

 

To determine if a function is Even or Odd graphically, just look at the function's graph.  If its graph is symmetrical with respect to the origin, it is Odd.  If its graph is symmetrical with respect to the y-axis, it is Even. 

 

To determine if a function is Even or Odd algebraically, you have to substitute in values for f(x).  If you substitute in -x for x in f(x) and get f(x)=f(-x) then the function is Even.  If you substitute in -x for x in f(x) and get f(-x)=-f(x) then the function is Odd.

 

In section 1.3 we covered Shifting, Reflecting, and Stretching Graphs

The basic function that is used for all transformations on a graph is

 

 

In this function,

a=vertical stretch/compress

b=horizontal stretch/compress

c=horizontal translation

d=vertical translation

 

Keep in mind that b is a stretch if it is less than 1, and a compress if greater than 1.  Also, a is a stretch if it greater than 1, and a compress if less than 1.

 

Consider the parent function

Its graph looks like this

All of the translations from the function  are represented on this graph

The parent function  is represented by the black in the middle.

The vertical shift of d is represented in red on the graph and is shifted down by -2.

The horizontal shift of c is represented in brown on the graph and is shifted right by 2.

The horizontal stretch of b is represented in blue on the graph by a factor of 1/2.

The vertical stretch of a is represented in green on the graph by a factor of 2.

 

Other than these transformations, graphs of functions can be reflected by being multiplied by a negative number.  For example the graph of in green looks like this compared to the parent function.

 

 

 

In section 1.4 we covered Combinations of Functions

There are four main combinations of functions.  These are the sum, difference, product, and quotient of functions.

 

Examples:  and

 

Sum:

                                

 

Difference:

                                          

      

Product:

                                    

 

Quotient:

                              = 5 remainder -8

 

These are the four basic combinations of functions.  Here are their definitions.

 

Another combination of functions is the composition of a function.

Definition:

The composition of the function f with g is =, the domain of f of g is the set of all the x in the domain of g such that g(x) is in the domain of f.

Example

 

   

=

             

                  

             

In section 1.5 we covered Inverse Functions

Inverse Functions:

 

 

There are two ways to verify inverse functions.  Algebraically and Graphically.  Graphically in order to verify an inverse function you need to graph the original function and the inverse function.  If their graphs are symmetrical among the line y=x then they are inverses of each other.  If they are not then the functions are not inverses of each other.  Algebraically involves creating a composition of the two functions that are in question.  If they both equal x then they are inverses of each other.  If it equals something else, then they are not inverses of each other.

 

Here is an example the book provides

 

Other than inverse functions in section 1.5, one-to-one functions are noted.

Definition of one-to-one:



A function f is one-to-one if, for a and b in its domain,  implies a=b

 

Also, a function only has an inverse if it is one-to-one.

If you substitute in a and b for x in a function and they end up equaling each other, then it is one-to-one.

 

To verify this graphically, use the horizontal line test.  This is similar to the vertical line test, except the line is horizontal.  If it intersects more than one point then the function is not one-to-one.