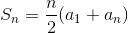9.2 Arithmetic Sequences

A sequence is arithmetic if the difference between consecutive terms is the same each time.
Arithmetic sequences have a common difference (d).
This means that:



An example of an arithmetic sequence would be
4,6,8,10,...

In this example, the common difference is 2.

The explicit formula for an arithmetic sequence is

The recursive formula for the previous example (4,6,8,10,...) would be

The sum of a finite arithmetic sequence is

Using the 4,6,8,10,... sequence with n=6, the sum would equal

= 54

7.3- Partial Fraction Decomposition

A rational expression can be written as the sum of two or more simpler rational expressions.
For example, this rational expression can be written like this:





The right side of the equation is called a partial fraction and together the whole equation makes up what is known as partial fraction decomposition. Partial fraction decomposition is a method to help break down a rational expression into simpler fractions.

How to Decompose Rational Expressions into Partial Fractions:

1. If the numerator's degree is greater than or equal to the denominator's degree, divide the numerator by the denominator.
2. Factor the denominator so it's irreducible and turned into factors of the expression.  
3. Split the factors up into a different partial fraction for each factor of the denominator. Each partial fraction should be with a constant numerator for each power of the factors in the denominator. Label the numerators with letters starting from A, B, C... depending on the number of partial fractions you have.
4. Set the two expressions equal to each other, the original rational expression and the new one with the sum of the partial fractions.
5. Clear the denominator by multiplying the equation by the least common denominator.
6. Simplify the equation and write in polynomial form.
7. You can equate coefficients of like terms on opposite sides of the equation and create a system of linear equations.
8. Solve the system of linear equations.
9. Substitute the values back into the original equation to obtain the partial fraction decomposition.

Here is an example:

  

and

Remember, if the degree of the numerator is greater than or equal to the degree of the denominator, then divide the numerator by the denominator using long division. The remainder is the rational expression used for the partial fraction decomposition.

Note: when there is repeated linear factors, like (x+1) to the second power, you would split that into two different partial fractions:

6.1 - Law of Sines

In the previous chapter we learned how to solve right triangles using trigonometry. Chapter 6 shows us how to solve for non-right triangles or otherwise known as oblique triangles.

To solve an oblique triangle, you need to know the measure of at least one side and any two other parts of the triangle - two sides, two angles, or one angle and one side. This breaks down into the following four cases

1. Two angles and any side (AAS or ASA)
2. Two sides and an angle opposite one of them (SSA)
3. Three sides (SSS)
4. Two sides and their included angle (SAS)

Below is how to derive the Law of Sines:

There are also an Ambiguous Case (SSA) in which there could be 2, 1, or no answer(s).

Below is a table to help determine the number of solutions there will be:

Area of an Oblique Triangle

Each triangle has a height of  h = b sinA and area of a triangle is A = 1/2*b*h

So, Area = 1/2 (c)(b sinA) = 1/2 bc sinA

You can also develop that: Area = 1/2 bc sinA = 1/2 ab sinC = 1/2 ac sinB

Law of Cosines (and Heron's Formula)

The Law of Cosines is an equation used to solve oblique triangles when given three sides or two sides and their included angle.

The equation can be derived in the following way.















This equation can be used to solve oblique triangles when the law of sines can not be used. For example, here is how the following triangle could be solved. (A triangle can also be solved using Law of Cosines when given two sides and their included angle.)

From the Law of Cosines, Heron's Area Formula is established. This formula can be used to find the area of an oblique triangle when only given sides of the triangle. To do this, the semiperimeter must be found. The semiperimeter is the sum of the three sides of the triangle divided by two, as shown in the picture below. The formula is as follows.










This formula can be used to find the area of an oblique triangle when given the side lengths. The side lengths can also be found using the Law of Sines or Law of Cosines. An example of how to find the area of a triangle is as followed, with the side lengths given.

Some More Trigonometric Formulas

Double- Angle Formulas:

These are used when you have a problem with a double angle (i.e. sin2x) and you want to put it in simpler terms so it is easier to solve.  

How to derive Double- Angle formulas:

 

 

Power- Reducing Formulas:
These are used when trying to get simplify a trig function that has been squared
WARNING: These are not necessarily helpful because they change the size of the angle.  They are not always a good idea to use, and they are not used often.  But we still have them because math.

 Half Angle Formulas
These are used to find angles that do not lie on the unit circle, but are half of an angle that does.

 

If you need a refresher on the sum and difference formulas, check out