For example, this rational expression can be written like this:

The right side of the equation is called a partial fraction and together the whole equation makes up what is known as partial fraction decomposition. Partial fraction decomposition is a method to help break down a rational expression into simpler fractions.
How to Decompose Rational Expressions into Partial Fractions:
1. If the numerator's degree is greater than or equal to the denominator's degree, divide the numerator by the denominator.
2. Factor the denominator so it's irreducible and turned into factors of the expression.
3. Split the factors up into a different partial fraction for each factor of the denominator. Each partial fraction should be with a constant numerator for each power of the factors in the denominator. Label the numerators with letters starting from A, B, C... depending on the number of partial fractions you have.
4. Set the two expressions equal to each other, the original rational expression and the new one with the sum of the partial fractions.
5. Clear the denominator by multiplying the equation by the least common denominator.
6. Simplify the equation and write in polynomial form.
7. You can equate coefficients of like terms on opposite sides of the equation and create a system of linear equations.
8. Solve the system of linear equations.
9. Substitute the values back into the original equation to obtain the partial fraction decomposition.
Here is an example:
 |
Remember, if the degree of the numerator is greater than or equal to the degree of the denominator, then divide the numerator by the denominator using long division. The remainder is the rational expression used for the partial fraction decomposition.
Note: when there is repeated linear factors, like (x+1) to the second power, you would split that into two different partial fractions:


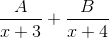



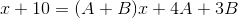






No comments:
Post a Comment