Section 1.5: Inverse Functions
What to know about inverse functions:
- How to find the inverse of a function algebraically.
- Verify if two functions are inverses of each other.
- How to use graphs to decide whether functions have inverses.
The notation for an inverse function is denoted as

IMPORTANT:
Do not get confused with the -1. This does not mean it is raised to the power of -1 nor does it take the reciprocal of the function. It is just the way to denote the inverse of a function. It is read as "f-inverse" or "the inverse of f."
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
The definition of the inverse function:
Let f and g be two functions that
 (For every x in the domain of f)
(For every x in the domain of f)If BOTH of these conditions are met, the function g is the inverse of f. The function of g can now be written as
 .
.So,

AND
 , and the range of f is equal to the domain of
, and the range of f is equal to the domain of .
.So what does this all mean?
Inverses have a way of undoing each other. When you plug one function into the other it will give you x. You must go through the order of operations in reverse order, known as SADMEP. All of the coordinates if plotted out will have the x and y coordinates switched. So (4,1) will be (1,4) in its inverse.
This is how you verify if two functions are inverses of each other.
EXAMPLE:
Show that the functions are inverses of each other.

SOLUTION:
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
The graph of an inverse function:
The graphs of f and
 are related in a graphical way. If there is a point (a, b) on a graph, then its inverse graphs (b, a). This is represented on the graph as the inverse of one graph reflected across the graph of y = x. (Shown Below)
are related in a graphical way. If there is a point (a, b) on a graph, then its inverse graphs (b, a). This is represented on the graph as the inverse of one graph reflected across the graph of y = x. (Shown Below)Not all graphs however have inverses. For example the parent function of

does not have an inverse with a domain of
 .
.To have an inverse, a function must be one-to-one.
The definition of a one-to-one function:
A function f is one-to-one if, for a and b in its domain,
f(a) = f(b) implies that a = b.
A function f has an inverse function
 if and only if f is one-to-one.
if and only if f is one-to-one.It is very easy to tell from a graph if a function is one-to-one. The Horizontal line test shows whether or not a function is one-to-one. If you draw a horizontal line anywhere on a graph and there is at most one point that intersects, then the function is one-to-one. If you notice that more than one point is created when drawing a horizontal line, then the function is not one-to-one and therefore does not have an inverse.
 |
| This function is not one-to-one since the horizontal line intersects at more than one point. |
There are two special types of functions that always pass the horizontal line test
- If f is increasing on its entire domain, f is one-to-one.
- If f is decreasing on its entire domain, f is one-to-one.
EXAMPLE:
Test to see if the function
 is one-to-one.
is one-to-one.ALGEBRAIC SOLUTION:
Let a and b be non negative real numbers with f(a) = f(b).
Therefore f(a) = f(b) implies a = b
So f is one-to-one.
GRAPHICAL SOLUTION:
How to find the inverse of a function:
To find the inverse of f, use the following steps,
- Use the Horizontal Line Test to decide whether f has an inverse.
- Substitute y for f(x) in the equation.
- Interchange the role of x and y and solve for y.
- Replace y with
 .
. - Show that f and
 are inverses of each other by showing that
are inverses of each other by showing that and
and
EXAMPLE:
The domain and range of f and its inverse consist of all real numbers so you must verify by completing step 5 (above).







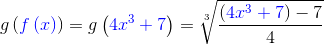
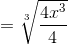


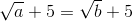



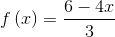


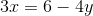



No comments:
Post a Comment