Smashing Functions
Arithmetic Combinations
Section 1.4
Just like we can combine real numbers using addition, subtraction, multiplication, and division, we can combine functions in the same way. There are four arithmetic operations (addition, subtraction, multiplication, division), so therefore there are four arithmetic combinations of functions. There are, however certain guidelines that must be followed with each combination in order to do them properly.
Here's our basic formulas:
Addition:

Subtraction:

Multiplication:

Division:
when
And here's how to combine our functions:
Addition
Example:
Given information:

Find
Think of this like f(x)+g(x). Since we know the values of f(x) and g(x) (as shown above), we can substitute in their values:
 |
| f(x) g(x) |
Subtraction
Example: Solve.

Think of this again like f(x)-g(x). Since we know the values of each of these we can substitute them in for f(x) and g(x):
*** most important step of subtracting functions***
DISTRIBUTE THE NEGATIVE:
Now combine like terms:
Multiplication
Example: Solve.

Find:
Think of this equation as f(x)*g(x), and substitute in the values of f(x) and g(x):
Now multiply while abiding to the math laws that be (in this case FOIL):
Division
Example: Solve.

Find:
Think of this as:
since we know the values of f(x) and g(x), we can substitute them in:
This specific problem is finished after substitution, but another may not be. If anything can be factored out and divided, you must do complete that step- otherwise, your problem is not finished.
With the division of functions, teachers and textbooks have a very common follow-up question:
What is the Domain of this function?
*see the blog post on section 1.1 for instructions on how to solve*
The domain of an arithmetic combination of functions f and g consists of all real numbers that are common to the domains of f and g. In the case of the division of functions, the denominator cannot equal zero.


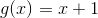
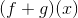
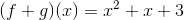






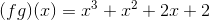



No comments:
Post a Comment