Chapter 1: Functions and Their Graphs

Today in class, we went deeper into section 1.1

1.1- Functions

 To most people, finding the slope of a straight line is very easy. All one has to do is find "rise over run" and 'voila', there is the slope. But how many times in a real-life situation is there going to be a straight-line graph? Let's just say that half the people around the world would either lose their job or get a decreased wage if this happened often. Employers wouldn't need to hire smart people if all they needed done was finding the straight line slope. Instead, most real-life graphs are curved which makes finding the slope a bit more of a challenge. Luckily, thanks to Issac Newton and Gottfried Leibniz for inventing calculus in the 17th century, we are able to find the slopes of curved graphs. 

One of the most basic definitions of calculus is called the difference quotient. 

  
Just like the equation to find the slope of a straight line, the difference quotient uses two points to find the slope at certain parts of a curved graph. The difference is that for a curved line, you are actually finding the slope of the secant line, or the line that passes through two points on the curve. If (x, f(x)) is the point of tangency and  (x+h, f(x+h) is the second point, then the difference quotient is the slope of the secant. Just like the slope of a straight line, the numerator is the change in y and the denominator is the change in x.  

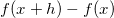Change in y

Change in x

Examples