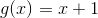Chapter 1: Functions and Their Graphs

Compositions of Functions

Just like arithmetic combinations of functions, you can also combine 2 functions by forming the composition of one with the other. In simpler terms, you take the f "of" g "of" x.

Example 1:

Solve for  

Given:

Solution:

To solve this problem, you substitute g(x) into f(x). 

Simplify:

Since you can plug one function into another, you can respectively plug a function into itself as well. 

Example 2: 

Solve for 

Given

To solve this problem, you plug the function into itself and take the g "of" g "of" x

*Important Reminders*

• f(g(x)) and g(f(x)) are not interchangeable because they don't always produce the same solution. 
• The open dot "o" and the multiplication dot "•" are different. 

Arithmetic Combinations

 Smashing Functions

Arithmetic Combinations

Section 1.4

 Just like we can combine real numbers using addition, subtraction, multiplication, and division, we can combine functions in the same way.  There are four arithmetic operations (addition, subtraction, multiplication, division), so therefore there are four arithmetic combinations of functions.  There are, however certain guidelines that must be followed with each combination in order to do them properly.

Here's our basic formulas:

 Addition:



 Subtraction:



 Multiplication:




Division:

when

And here's how to combine our functions:

Addition

                                            

Example: 

 Given information:                                      

Find

Think of this like f(x)+g(x).  Since we know the values of f(x) and g(x) (as shown  above), we can substitute in their values:

                                        f(x)                  g(x)

                                              Now all you have to do is combine like terms:

    

Subtraction

Example: Solve.         

 Given information:                                      

                                                                             Find: 

 Think of this again like f(x)-g(x).  Since we know the values of each of these we can substitute them in for f(x) and g(x):

*** most important step of subtracting functions***

DISTRIBUTE THE NEGATIVE:

 

 Now combine like terms:

Multiplication

Example: Solve.         

 Given information:                                      

Find:

  Think of this equation as f(x)*g(x), and substitute in the values of f(x) and g(x):

Now multiply while abiding to the math laws that be (in this case FOIL):

Division

Example: Solve.         

 Given information:                                      

 Find:

 Think of this as:

 since we know the values of f(x) and g(x), we can substitute them in:

This specific problem is finished after substitution, but another may not be.  If anything can be factored out and divided, you must do complete that step- otherwise, your problem is not finished.  

With the division of functions, teachers and textbooks have a very common follow-up question:

What is the Domain of this function?

*see the blog post on section 1.1 for instructions on how to solve*

 The domain of an arithmetic combination of functions f and g consists of all real numbers that are common to the domains of f and g.  In the case of the division of functions, the denominator cannot equal zero.

Chapter 1: Functions and Their Graphs

Today in class, we reviewed shifting, reflecting, and stretching/shrinking.

At this point in the trimester, our class has only began to scratch the surface of the importance of functions and their graphs. We have already discussed the basics of functions: how functions are defined, what they look like, the domains and ranges of these function, and how to graph simple functions. Today, we reviewed a familiar, but extremely important aspect of functions-- how to manipulate them.


For each manipulation, consider this parent function and its graph:

SHIFTING:

In order to vertically shift any graph (either up or down), remember the equation:



**C, a constant, affects the output value in this equation, not the input value**

C > 1  Graph shifts upwards

C < 1  Graph shifts downward

EXAMPLE: Shiftup two units. Graph the parent function in blue and the new function in green

In order to horizontally shift any graph (either left or right), remember the equation:



**C affects the input value in this equation, not the output value**

C is a positive number  Graph shifts to the left

C is a negative number  Graph shifts to the right


EXAMPLE: Shiftleft two units. Graph the parent function in blue and the new function in green

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -  

REFLECTING:

In order to vertically reflect any graph across the x-axis, remember the equation:




*Because the negative is applied to f(x), only the output values are affected whereas the input values remain the same*

EXAMPLE: Reflectacross the x-axis. Graph the parent function in blue and the new function in green

*Notice how the inputs (x values) remain the same while the outputs (y values) are multiples by -1*


In order to horizontally reflect any graph across the y-axis, remember the equation:



*Because the negative is applied to (x), only the input values are affected whereas the output values remain the same*

EXAMPLE: Reflectacross the y-axis. Graph the parent function in blue and the new function in green

WHY DOES THIS GRAPH LOOK THE SAME AS THE FUNCTION?! Because reflecting the parent function over the y-axis yields the exact same graph :)



- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -  

STRETCHING/SHRINKING:

Remember, stretching and shrinking distorts the graph (changes its original shape)!

In order to vertically stretch/shrink any graph, remember the equation:





**C affects the output value in this equation, not the input value**

C > 1  Vertical stretch-- getting closer to the y-axis

0 < C < 1  Vertical shrink-- getting farther away from the y-axis

Vertical Stretch: by a factor of 2

Vertical Shrink: by a factor of 1/2

In order to horizontally stretch/shrink any graph, remember the equation:


**C affects the input value in this equation, not the output value**

C > 1  Horizontal shrink-- getting farther away from the x-axis

0 < C < 1  Horizontal stretch-- getting closer to the x-axis


Horizontal Shrink: by a factor of 2

Horizontal Stretch: by a factor of 1/2

OVERALL: 

Perhaps the most important equation you can take away from this lesson is this one:

a= Vertical stretch/shrink (stretch: c>1 shrink: 0<c<1)

b= Horizontal stretch/shrink (stretch: 0<c<1  shrink c>1)

c= Horizontal translation (left or right)

d= Vertical translation (up or down)

This equation sums up everything we discussed in today's class in a neat and concise manner!

Hope this helps! Good luck in Honors Pre-Calc :)