3.1 Exponential Functions and Their Graphs
Properties of Exponents:
When you multiply two terms, you add the exponents
When you divide two terms, you subtract the exponents
When you raise a power to a power, you multiply the exponents
Exponents to the power of n:
Properties of an exponential function:
x-intercept: none
y-intercept: (0,1)
Vertical Asymptote: none
In the function above, the graph approaches the line y=0 and intersects the y-axis at (0,1).
Shifting, Reflecting, and Stretching Exponential Functions
- a represents a vertical stretch or compress, if a is negative, the graph reflects in the x-axis
- b will make the graph's rate increase faster or slower
- c will shift the graph left or right
- d will shift the graph up or down
One-to-One Property
If the equation has the same base on both sides, the exponents can be set equal to each other and solved for x.
Example:
Since both sides have a base of 5, the exponents can be set equal to each other to solve for x.
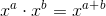











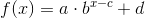



No comments:
Post a Comment