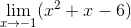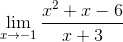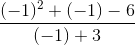12.4 Limits at Infinity/Sequences

12.4 Limits at Infinity and Limits of Sequences

The limit as x approaches infinity is just talking about end behavior

Step 1: plug in massive number into your equation

Step 2: get answer

Step 3: that answer is the limit at infinity

In sequences An is the same as f(x) 

When in doubt one can always plug numbers in

That wouldn't work if one would get 0/0 because that means indeterminate

12.3 The Tangent Line Problem

Slope 

The slope m of the graph f at the point (x,f(x)) is equal to the slope of its tangent line at (x,f(x)), and is given by:

which is equal to the difference quotient

Finding Slope of a Graph

Derivatives

The derivative of f at x is 

provided this limit exists

12.2 Techniques for Evaluating Limits

Techniques for Evaluating Limits

There are a few ways to evaluate limits. Based on the given function, you need to decide which technique to use. As we learned before, limits are very well behaved when it comes to manipulating the function. That means that you can multiply, divide, subtract, raise to a power, etc. without having to alter the function. This is one way that makes limits easier.

Limits are defined as:

Continuous functions are defined as:

THIS DEFINITION IS NOT IN THE BOOK!!

One way to evaluate limits is by direct substitution.

Direct Substitution

If you are given a function f(x) that is a simple polynomial then you can just plug c into it to find the limit f(c). This also works with rational functions when the denominator is not equal to 0. 

____________________________________________

Dividing Out Technique

NOTE: When using the dividing out technique, if you get 0 in the denominator, then the limit does not exist!

If we wanted to evaluate the limit above as x approaches -3, we would not be able to do that since the denominator would equal 0. However, if you graphed the function you would see that the limit is -5. This is when the dividing out technique can be used. 

(Divide out the x+3)

(Now you can use the direct substitution method)

The only graphical difference between  and  is the hole in the graph.

You should only use the dividing out technique when you get 0 on the top and on the bottom after substitution of c. Otherwise you should use a different technique. 

Rationalizing Technique

The rationalizing technique can be used in the same way as the dividing out technique. That is when you get 0 on the top and bottom. However, when you can't divide common factors, you use this over the divide out technique. 

When you plug in c for the initial limit you will see that you get the indeterminate form (0/0) but when you do the same for the limit that we rationalized you get 1/2. That is how the rationalization form is used. Remember when you multiply by the conjugate you get the difference of squares. {(a+b)(a-b) = (a² - b²)}

12.1 Limits!

Definition: If f(x) becomes arbitrarily close to a unique number L as x approaches c from either side, the limit of f(x) as x approaches c is L

This is written as

For most cases, you can find the limit by simply substituting c in for x.

Example:

As x approaches 2 on both sides, it is getting closer to 9. This can be confirmed using a graphing utility.


However, substituting the number can give you an undefined answer.
Example:

Since you are finding the limit as x approaches 2,  you can use the table feature on your graphing calculator and create a table that shows the value of the function for x beginning at 1.9 and increasing by 0.01.

From the table, you can estimate the limit to be 5. In this case, you can't obtain the limit by evaluating f(x) when x=2


LIMITS THAT DON'T EXIST

Condition Under Which Limits Do Not Exist

1) f(x) approaches a different number from the right side of c than from the left side of c
2) f(x) increases or decreases without bound as x approaches c
3) f(x) oscillated between two fixes values as x approaches c

In simpler terms:
1) If there is a break in the graph
2) If it goes to infinity
3) If it oscillates (sin)


Example 1: 

In this example, as x approaches 0, y will get closer to two different numbers. Therefore, the limit does not exist.


Example 2:

On the graph 1/x^2, the limit as x approaches 0 does not exist. Although it approaches infinity, infinity is not a real number. It doesn't approach a particular value.


Example 3:

The graph above represents sin(1/x). No matter how close x approaches 0, f(x) always oscillates between 1 and -1. f(x) is not approaching a certain value so the limit does not exist.

10.7 Graphs of Polar Functions

Just like any other function (quadratic, logarithmic, etc.), polar functions have certain rules and characteristics that govern their symmetry, shifting, asymptotes, periods, shifts, and general shape.

A simple way to quickly determine the shape of a polar graph without the aid of a graphing calculator is to plot its points:

	0	π/6	π/3	π/2	2π/3	5π/6	π	7π/6	3π/2	11π/6	2π
r	0	2	2√3	4	2√3	2	0	-2	-4	-2	0

Quickly plotting points as show above allows a quick sketch of the graph to be drawn:

In general, however, all simple sine and cosine polar equations of the form r = acos(θ) or r = asin(θ) will be circles with a diameter of a that are either tangent to the polar axis and symmetric with respect to the line θ = π/2 (sine functions) or tangent to the line θ = π/2 and symmetric with respect to the polar axis (cosine functions).

There are three important types of symmetry to consider that can make graphing or predicting the shape of a polar function much easier.

Figure A: This is a polar function that is symmetric with respect to the line θ = π/2 (the cartesian y-axis). This can be tested for algebraically by replacing (r, θ) with either (r, π - θ) or (-r, -θ). If this substitution results in an equivalent equation, the equation is symmetric with respect to θ = π/2.

Figure B: This is a polar function that is symmetric with respect to the polar axis (the cartesian x-axis). This can be tested for algebraically by replacing (r, θ) with either (r, -θ) or (-r, π - θ). If this substitution results in an equivalent equation, the equation is symmetric with respect to the polar axis. 

Figure C: This is a polar function that is symmetric with respect to the pole (the origin). This can be tested for algebraically by replacing (r, θ) with either (r, π + θ) or (-r, θ). If this substitution results in an equivalent equation, the equation is symmetric with respect to the pole.

Special Polar Graphs:

Limaçons and cardioids with the form r = a ± bcos(θ) or r = a ± bsin(θ) where a > 0 and b > 0:

(A)(B)(C)    (D)

Figure A: This limaçon with the equation r = 1 + 2cos(θ) is  looped because a/b < 1.

Figure B: This cardioid with the equation r = 1 + cos(θ) is heart-shaped because a/b = 1.

Figure C: This limaçon with the equation r = 3 + 2cos(θ) is dimpled because 1 < a/b < 2.

Figure D: This limaçon with the equation r = 4 + 2cos(θ) is convex because a/b ≥ 2.

Rose curves with the form r =  acos(nθ) or r = asin(nθ) where n is an integer and a is the length of each petal:

(A)(B)

(C)(D)

Figure A: This rose curve with the equation r = cos(3θ) has 3 petals because n = 3. When rose curves have n as an odd number, the number of petals will equal n.

Figure B: This rose curve with the equation r = cos(4θ) has 8 petals because n = 4. When rose curves have n as an even number, the number of petals will equal 2n.

Figure C: This rose curve with the equation r = sin(5θ) has 5 petals because n = 5.

Figure D: This rose curve with the equation r = sin(2θ) has 4 petals because n = 2.

As a rule, rose curves are symmetric to the polar axis, the line θ = π/2, and the pole and have zeroes when r = 0 or θ = π/4, 3π/4.


Lemniscates with the form r² = a²sin(2θ) or r² = a²cos(2θ) where a is the length of each protrusion:

(A)(B)

Figure A: This lemniscate with the equation r² = sin(2θ) is mostly contained in the first and third quadrants due to the sine in its equation.

Figure B: This lemniscate with the equation r² = cos(2θ) lies equally in all four quadrants due to the cosine in its equation.

As a rule, lemniscates are symmetric with respect to the pole and have zeroes when θ = 0, π/2.